Contents

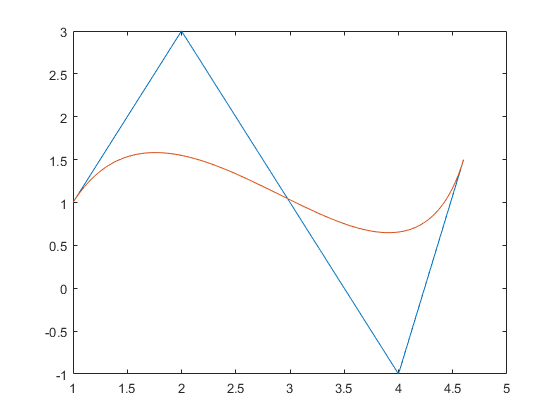
Ejercicio 1

% %bernstein.m
% function b=bernstein(n,i,t)
% b=combina(n,i).*t.^i.*(1-t).^(n-i);
% end
%
% %combina.m
% function c=combina(n,i)
% c=factr(n)/(factr(i)*factr(n-i));
% end
%
% %factr.m
% function f = factr(n)
%     if n==0
%         f = 1;
%     else
%         f = n*factr(n-1);
%     end
% end

% %graf_berstein.m
% t=linspace(0,1);
% n=3;
% for i=0:n
%     b=bernstein(n,i,t);
%     plot(t,b);
%     hold on;
% end
% xlabel('t');
% ylabel('Polinomio de Bernstein');
% title('Polinomio Bernstein grado 3');
% legend('B3,0','B3,1','B3,2','B3,3');

%graf_bezier
t=linspace(0,1);
V=[1 2 4 4.6;1 3 -1 1.5];
plot(V(1,:),V(2,:));
n=size(V);n=n(2);
s=size(t);s=s(2);
x=zeros(n,s);y=zeros(n,s);
for i=1:n
    x(i,:)=bernstein(n-1,i-1,t)*V(1,i);
    y(i,:)=bernstein(n-1,i-1,t)*V(2,i);
end
a=sum(x);b=sum(y);
hold on;
plot(a,b);

Ejercicio 2

%viento.m
clear,clc

velocidad=xlsread('sotaventogaliciaanual','Hoja1','B2:B52129');
%interpolar si es necesario
if any(isnan(velocidad)) %si hay algún NaN
    x=1:length(velocidad);
    i=find(~isnan(velocidad));
    velocidad=interp1(x(i),velocidad(i),x);
end
%histograma
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);

%convierte a frecuencias y ajusta a la función de Weibull
frec=horas/sum(horas);
f=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
a0=[2 8];  %valor inicial de los parámetros
af=nlinfit(x,frec,f,a0)
hold on

%diagrama de frecuencias
bar(x,frec,'c');

%representa la curva de ajuste
x=linspace(0,max(velocidad),100);
y=f(af,x);
plot(x,y,'r')

title('Ajuste a la función Weibull')
xlabel('Velocidad')
ylabel('Frecuencia')
hold off

%viento2.m
%directamente de los datos de las velocidades del viento
potencia=0.5*1.225*sum(velocidad.^3)/length(velocidad);
fprintf('Potencia, directamente de las medidas: %3.1f\n',potencia);
media=mean(velocidad);
%función de distribución de Weibull

% Parametros de ajsute de Weibull:
k=2.0486;c=9.4165;

potencia=0.5*1.225*media^3*gamma(1+3/k)/(gamma(1+1/k)^3);
fprintf('Potencia, función Weibull: %3.1f\n',potencia);
%función de distribución de Rayleigh
potencia=0.5*1.225*6*media^3/pi;
fprintf('Potencia, función Rayleigh: %3.1f\n',potencia);

Pr=1500; x0=3.0;xr=14;x1=25; %datos de la curva de potencia
potencia=xlsread('sotavento_curva potencia','Hoja1','B2:B27')
x=0:0.5:25;
pot=potencia(x>=3 & x<=12);
hold on
x=x0:0.5:xr-2;
plot(x,pot,'ro','markersize',3,'markerfacecolor','r')
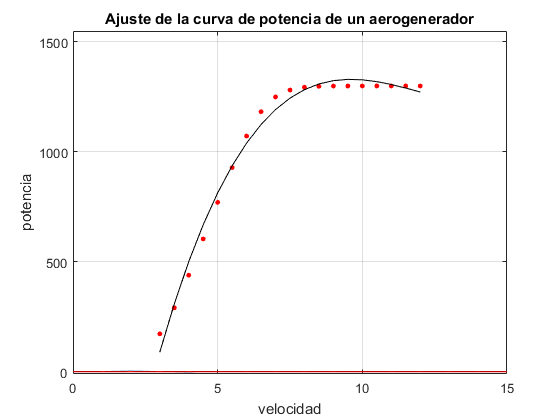
title('Ajuste de la curva de potencia de un aerogenerador');
axis([0 15 -10 1550])
xlabel('velocidad')
ylabel('potencia')
grid on

%ajuste
p=polyfit(x,pot',3); %ajuste a un polinomio de tercer grado
yp=polyval(p,x);
plot(x,yp,'k')
hold off
%cálculo de la potencia media
f=@(x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k); %función de Weibull
h=@(x) f(x).*polyval(p,x);
power=quad(h,x0,xr)+Pr*quad(f,xr,x1);
fprintf('La potencia media es: %3.1f\n',power)

af =

    2.3849    6.0208

Potencia, directamente de las medidas: 187.8
Potencia, función Weibull: 194.0
Potencia, función Rayleigh: 198.6

potencia =

   1.0e+03 *

         0
         0
         0
         0
    0.0321
    0.0916
    0.1725
    0.2912
    0.4393
    0.6043
    0.7706
    0.9287
    1.0722
    1.1831
    1.2501
    1.2817
    1.2940
    1.2982
    1.2995
    1.2998
    1.3000
    1.3000
    1.3000
    1.3000
    1.3000
    1.3000

La potencia media es: 1028.4

Ejercicio 3

% %funcion_sistema.m
% function dxdt = odefun(t,x)
% m=20;k=20;c=5;
% dxdt = [x(2);-(1/m)*(c*x(2)+k*x(1))];
%
% %funcion_sistema2.m
% function dx2dt = funcion_sistema(t,x)
% m=20;k=20;c=40;
% dx2dt = [x(2);-(1/m)*(c*x(2)+k*x(1))];
%
% %funcion_sistema3.m
% function dx2dt = funcion_sistema(t,x)
% m=20;k=20;c=200;
% dx2dt = [x(2);-(1/m)*(c*x(2)+k*x(1))];

%funcion_ode.m
t0=0;tf=40;
periodo=[t0 tf];
cond_inicio=[1 0];
[t,x] = ode45('funcion_sistema',periodo,cond_inicio);
plot(t,x(:,1),'-o')
hold on
[t,x] = ode45('funcion_sistema2',periodo,cond_inicio);
plot(t,x(:,1),'-+')
[t,x] = ode45('funcion_sistema3',periodo,cond_inicio);
plot(t,x(:,1),'-*')
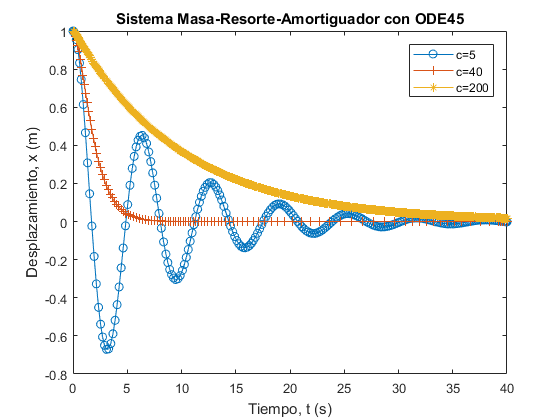
title('Sistema Masa-Resorte-Amortiguador con ODE45');
xlabel('Tiempo, t (s)');
ylabel('Desplazamiento, x (m)');
legend('c=5','c=40','c=200')

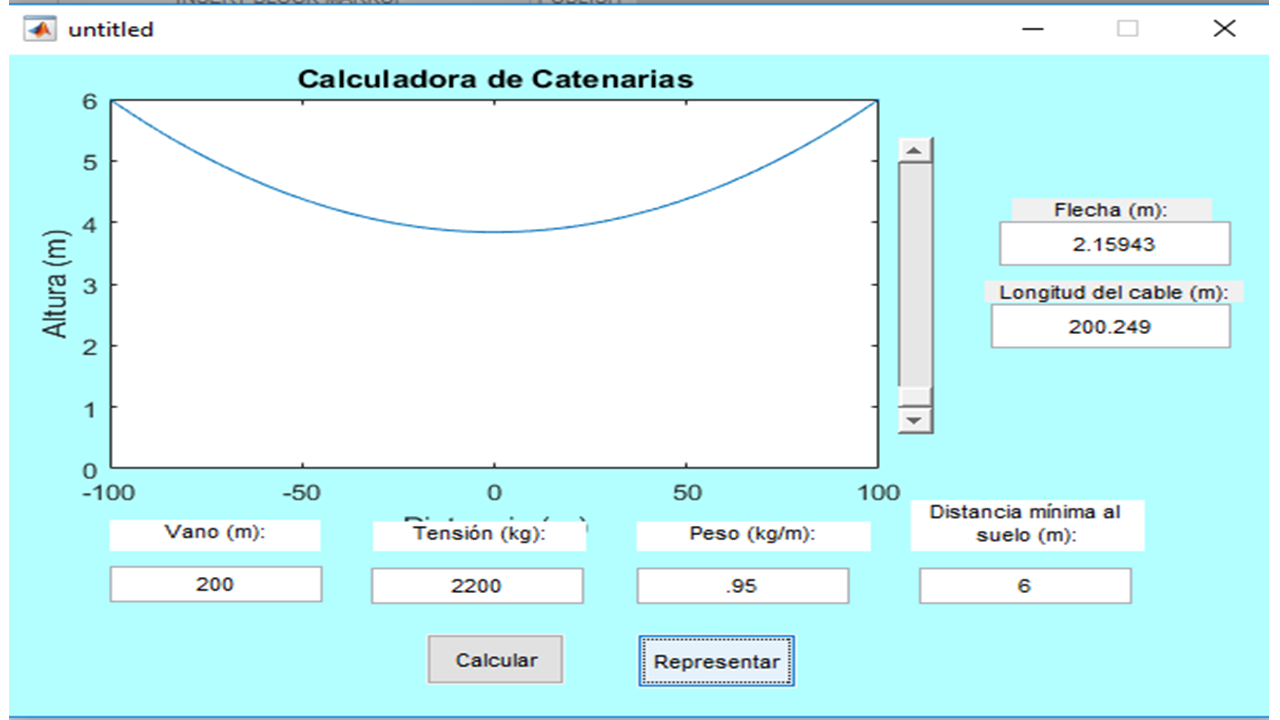
Ejercicio 4

%untitled.m

Published with MATLAB® R2017a